ACTIVIDAD 4

ÁREA BAJO UNA CURVA

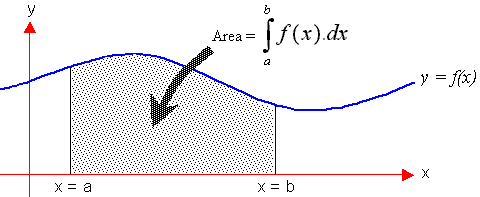
La formulación del área bajo una curva es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.

Si hacemos más pequeño la anchura del rectángulo, entonces el número N es mas grande y mejor la aproximación al valor del área.

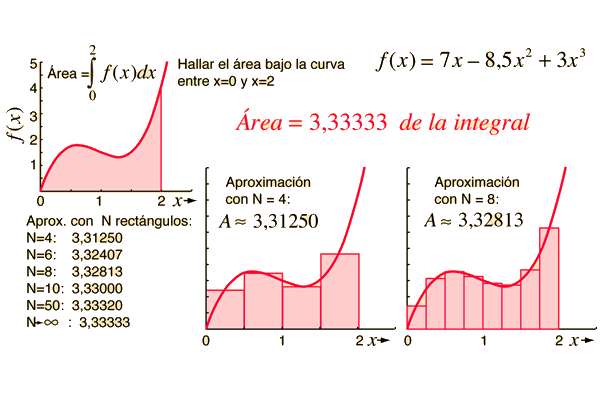
Sumas de Riemann con un número "infinito" de rectángulos

Imagina que queremos encontrar el área bajo la gráfica de $f(x)=\dfrac15x^2$f, left parenthesis, x, right parenthesis, equals, start fraction, 1, divided by, 5, end fraction, x, squared entre $x=2$x, equals, 2 y $x=6$x, equals, 6.

Usando la notación de integral definida, podemos representar el área exacta como:

$\displaystyle\int_2^6 \dfrac15 x^2\,dx$integral, start subscript, 2, end subscript, start superscript, 6, end superscript, start fraction, 1, divided by, 5, end fraction, x, squared, d, x

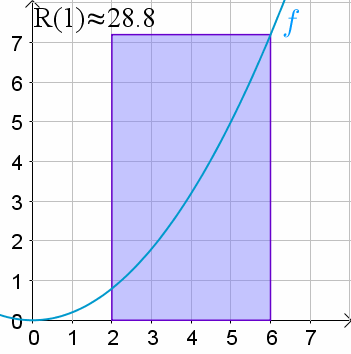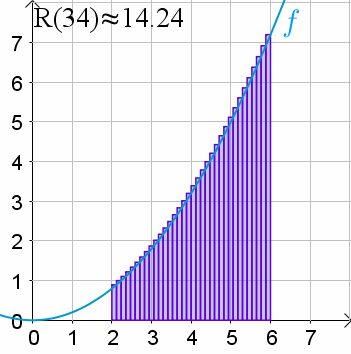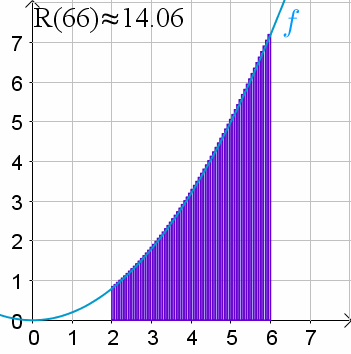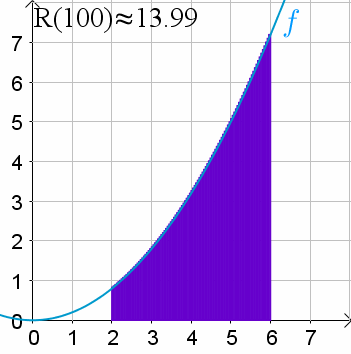
Podemos aproximar esta área mediante sumas de Riemann. Sea $R(n)$R, left parenthesis, n, right parenthesis la aproximación por suma de Riemann derecha con $n$n subdivisiones (es decir, $n$n rectángulos de ancho igual).

Por ejemplo, la gráfica muestra $R(4)$R, left parenthesis, 4, right parenthesis. Puedes observar que es una sobrestimación del área real.

$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$y$$x$$\blueD{f}$

El área bajo la curva de $f$f entre $x=2$x, equals, 2 y $x=6$x, equals, 6 se aproxima por medio de $4$4 rectángulos de bases iguales.

Podemos mejorar nuestra aproximación al dividir nuestra área en más rectángulos con bases menores, es decir, al usar $R(n)$R, left parenthesis, n, right parenthesis con valores mayores de $n$n.

Puedes observar cómo la aproximación se acerca más al área real conforme el número de rectángulos va de $1$1 a $100$100:

Creado con Geogebra.

Por supuesto, usar aún más rectángulos nos acercará aún más, pero una aproximación siempre es solo una aproximación.

¿Qué tal que pudiéramos considerar una suma de Riemann con un número infinito de subdivisiones iguales? ¿Acaso es eso posible? Bueno, no podemos tomar $n=\infty$n, equals, infinity porque el infinito no es un número, pero tal vez recuerdes que tenemos una forma de llevar algo a infinito...

EJEMPLOS DE ÁREA BAJO CURVA 

1 Calcular el área del recinto limitado por la curva  y el eje .

1 En primer lugar hallamos los puntos de corte con el eje  para representar la curva y conocer los límites de integración.

2 En segundo lugar se calcula la integral:

2 Hallar el área de la región del plano encerrada por la curva  entre el punto de corte con el eje  y el punto de abscisa .

1 En primer lugar calculamos el punto de corte con el eje de abscisas.

2 La integral se resuelve mediante integración por partes

3 Hallar el área limitada por la recta , el eje  y las ordenadas de  y .

Hallar el área limitada por la recta , el eje  y las ordenadas de  y .

4 Calcular el área limitada por la curva  y el eje de abscisas.

1 Calculamos los cruces de la función con el eje de las abscisas

 

2 Planteamos y resolvemos la integral definida

 

5 Calcular el área de las regiones del plano limitada por la curva  y el eje .

1 Calculamos los cruces de la función con el eje de las abscisas

2 Planteamos una integral definida

hernandez olivera pedro